燃气轮机连接结构的存在使得转子系统的动力学特性变得复杂。不同于连续转子，拉杆转子在结构上不是一个连续的整体。尤其在预紧力松弛的情况下，采用基于连续转子的建模方法对拉杆转子进行分析得到的结果与实验结果会存在较大差异。因此，需要建立拉杆转子接触界面的力学模型，并在分析其转子动力学特性中考虑接触界面连接刚度，获得适合拉杆转子的建模方法。 

　　本实验室研究人员使用六自由度弹簧单元同时等效盘盘接触刚度与拉杆弯曲刚度，分别描述接触界面三个平动方向与三个转动方向的自由度，并用两个6×6的矩阵分别表示其刚度和阻尼。提出了一种考虑连接刚度的复杂转子轴系动力学计算方法，计算了某周向拉杆转子的动态特性。 

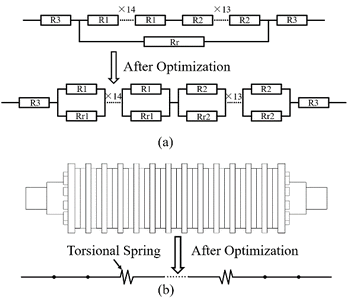
　　图1  连接刚度等效方法 

　　研究发现，随着刚度的减小，临界转速与振动响应幅值都在不断减小。其中：临界转速下降呈现先缓后急的趋势，即在开始阶段缓慢减小，逐渐增大下降速度；而响应的减小呈现先急后缓的趋势（如图2），即在开始阶段显著下降，而后下降速率减缓。值得注意的是：在图2中的二阶转速响应上，10次方的响应大于11次方，经验证此时的弯曲振型发生了改变。 

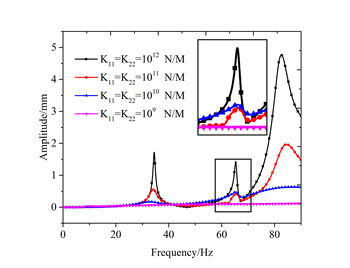
　　图2  不同连接刚度下的响应 

　　通常情况下，燃机转子不会有显著的非对称刚度，但在某些故障模式或极端运行条件中，也存在该类型失稳的可能性。例如：非均匀温度场引起的周向拉杆预紧力分布不均匀、以及某根拉杆发生断裂等。本文基于六自由度弹簧的连接刚度等效方法可以方便地研究转子在该失谐下的动力学特性。 

　　研究人员分别计算了各向异性剪切刚度与各向异性弯曲刚度两种失谐类型。临界转速对应的响应峰值均在一个方向上分裂为两个峰值。对于各向异性剪切刚度，该分裂方向为小刚度对应方向；而对于各向异性弯曲刚度，该分裂方向为大刚度对应方向。且峰值分裂方向的响应幅值要小于其正交方向。此时，转子在同一阶两个临界转子，轴心轨迹变为椭圆(如图3)，椭圆的长半轴受小刚度影响，长半轴受大刚度影响，当两正交刚度相差越大时，椭圆的椭圆度也越大，且θ角也随之增大。 

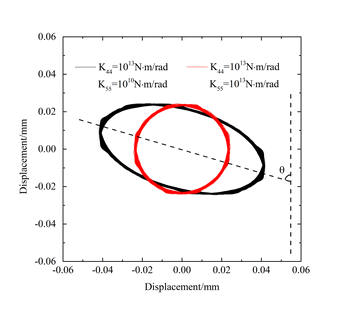
　　图3  刚度不对称时的轴心轨迹 

　　根据以上由等效方法计算得到的结果，研究人员提出几种针对连接刚度的振动抑制方法：（1）保持盘与盘间的刚性连接，设置一定的预紧力过盈量，尽量让拉杆预紧力处于未松弛状态；（2）尽量减少不均匀分布的温度场，排除预紧力失谐的可能性；（3）减小轮盘偏心量，改变接触面状态，增加连接界面的无量纲阻尼。