近期，中科院工程热物理研究所风能利用重点实验室/国家能源风电叶片研发（实验）中心在风电机组尾流解析建模方法上开展了深入研究，提出将尾流模型的扩张系数与展向湍流强度建立联系，并引入经典的MOST理论，建立了一个新的MOST-Gaussian尾流模型。通过与高精度数值仿真数据和实验数据进行对比，验证了新模型对尾流速度亏损具有很好的预报能力。相较于传统尾流模型，MOST-Gaussian模型能应用于不同的地表粗糙度和大气稳定度条件，对于精确的风电场微观选址和尾流控制具有重要意义。上述研究结果发表于国际能源期刊Applied Energy，被风能研究领域的多位著名学者引用。 

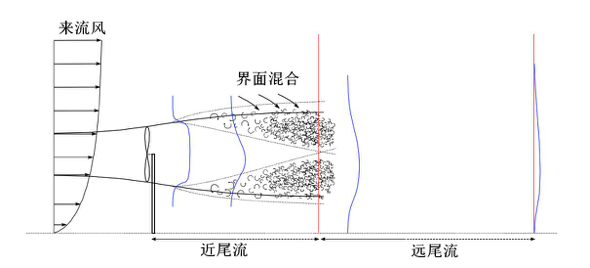
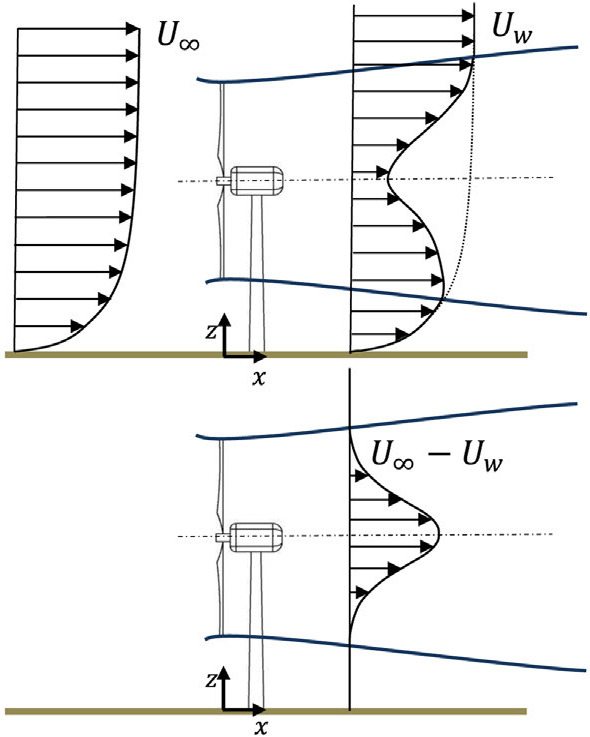
　　在风力发电行业，通常将风轮下游的流场称为尾流，如图1所示。风电机组下游的尾流可以分为近尾流区域和远尾流区域。近尾流区域的长度一般为1~2倍叶轮直径，速度和湍流强度分布与风轮的叶片数、叶片气动参数及叶尖涡发展有密切关系。远尾流区域的长度可以达到10~15倍风轮直径，流场分布受风轮的几何结构影响较小，速度分布接近于高斯分布，呈现出一定的自相似性，如图2所示。 

　　通过假定速度亏损满足高斯分布，国外文献报道了一种二维尾流模型，预测的速度分布和实验结果与大涡模拟结果吻合得非常好，然而模型中的尾流扩张系数需要通过对实验结果或者仿真数据进行拟合才能得到，通用性较差。为解决这一问题，基于大气边界层中经典的Monin-Obukhov相似性理论（MOST）提出了一个MOST-Gaussian尾流模型。 

　　MOST-Gaussian尾流模型主要有两个方面的创新。首先假定尾流扩张系数与展向湍流强度相关。传统高斯模型认为尾流扩张系数与流向湍流强度有关，然而风洞实验和数值仿真均表明尾流通常在展向和法向扩张，即尾流恢复主要与展向和法向的动量输运密切相关，因此MOST-Gaussian模型的假设更为合理。另一个创新之处是通过引入MOST理论，新模型将地表粗糙度和大气稳定度作为输入参数，可以研究不同环境条件下尾流发展的规律，拓展了模型的应用范围，使得模型具有更好的通用性。 

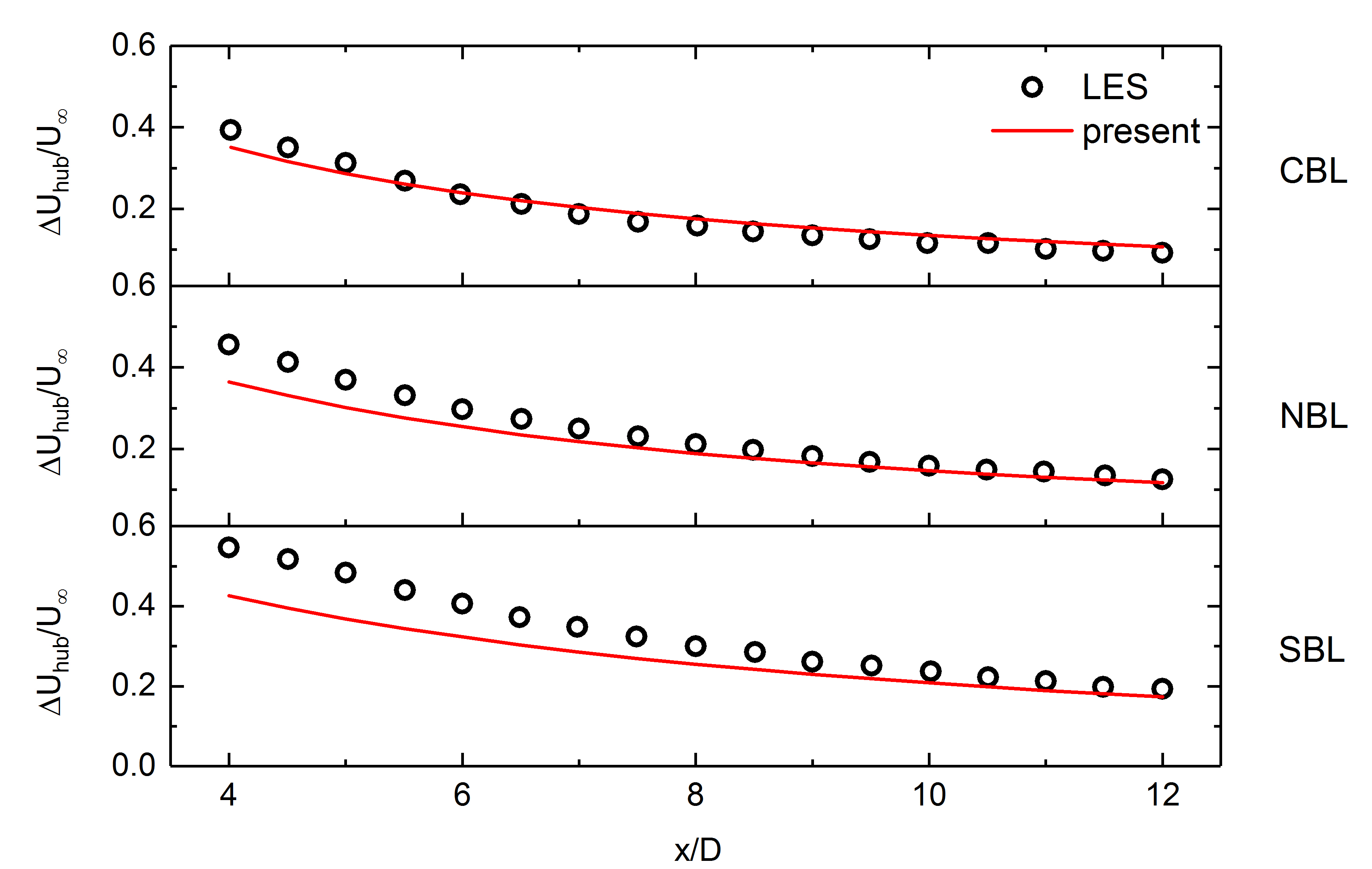
　　将MOST-Gaussian尾流模型预测的结果与文献中报道的其他模型进行了对比，轮毂高度不同下游位置的速度亏损如图3所示。对比结果表明不同地表粗糙度下新模型具有更好的预测精度。与文献报道的模型不同，MOST-Gaussian模型能够预测不同大气稳定度下的速度亏损，如图4所示。从图中可以看出新模型能较好地反映不同稳定度下尾流的演化情况。 

　　对风电机组的近尾流区域进一步分析，可以发现速度亏损剖面表现出两个峰值，利用双峰高斯分布函数可以更为精确地表征近尾流的特点，同时双峰高斯分布函数可以退化成常规的单峰值分布，因此在远尾流区域退化成MOST-Gaussian尾流模型，表明双峰高斯分布模型在尾流速度分布预测方面具有很大的潜力。 

　　上述研究结果发表于Applied Energy杂志，被风能研究领域的多位著名学者引用。论文第一作者为工程热物理研究所的博士生程瑜，通讯作者为工程热物理研究所张明明研究员。 

　　DOI: 10.1016/j.apenergy.2019.01.225 

　　论文链接: https://www.sciencedirect.com/science/article/abs/pii/S0306261919302454 

　　图1 风电机组尾流结构

　　图2 高斯分布形式的速度亏损

　　图3 轮毂高度处不同下游位置的速度亏损对比

　　图4 不同大气稳定度下轮毂高度的速度亏损